Airfoil Maker Manual
Last updated:
About This Manual
This is version 12 of the manual to Airfoil Maker. The latest version of the manual will always be available from the X‑Plane Developer web site.
Throughout this text, there will be cross-references to other parts of the manual, as well as hyperlinks to web pages. These will be formatted as blue text. The Table of Contents is also cross-referenced; click on the section you’re looking for to travel there instantly. To search for a specific term or set of words, press “ctrl” (“command” on a Mac) + “f” to be taken to the term anywhere in the document. For a PDF version of this manual, use an HTML to PDF converter such as pdfcrowd.com.
This manual, like all X‑Plane documentation, is released under the Creative Commons Attribution-ShareAlike 2.5 license. This means you are free to copy, share, and adapt the works so long as you give Laminar Research (creators of X-Plane) credit and release your work under a similar license.
For the most part, this manual assumes basic knowledge of the X‑Plane user interface-in particular, it assumes knowledge of how to open and fly an aircraft.
Introduction
The menus of Airfoil Maker are very simple.
About: The About menu’s only option, Version, will display the version of the program and check for updates from the X-Plane.com website.
File Menu: The file menu works just like the file menu of any word processor or spreadsheet application. Files are created, loaded, and saved here; the only difference is that, instead of text documents, Airfoil Maker is opening and saving files that represent airfoils.
New: Use this to generate a new airfoil.
Open: Use this to open an existing airfoil for viewing or modification.
Save: Use this to save an airfoil that was created or modified.
Save As: Use this to save an airfoil that was created or modified under a different name.
Convert All Airfoils to Latest Format: Use this for the program to automatically update any airfoils that were designed for X‑Plane version 7 or earlier so they are compatible with the latest version of the simulator.
Quit: Exit Airfoil Maker.
Designing an Airfoil
Every airfoil ever designed has its own specific characteristics, which are its coefficients of
- how much the airfoil wants to lift up,
- how much the airfoil wants to pull back, and
- how much the airfoil wants to pitch up.
The Coefficient Graph
Dominating the design screen is a large black graph with green, red, and yellow lines on it, like Figure 1.
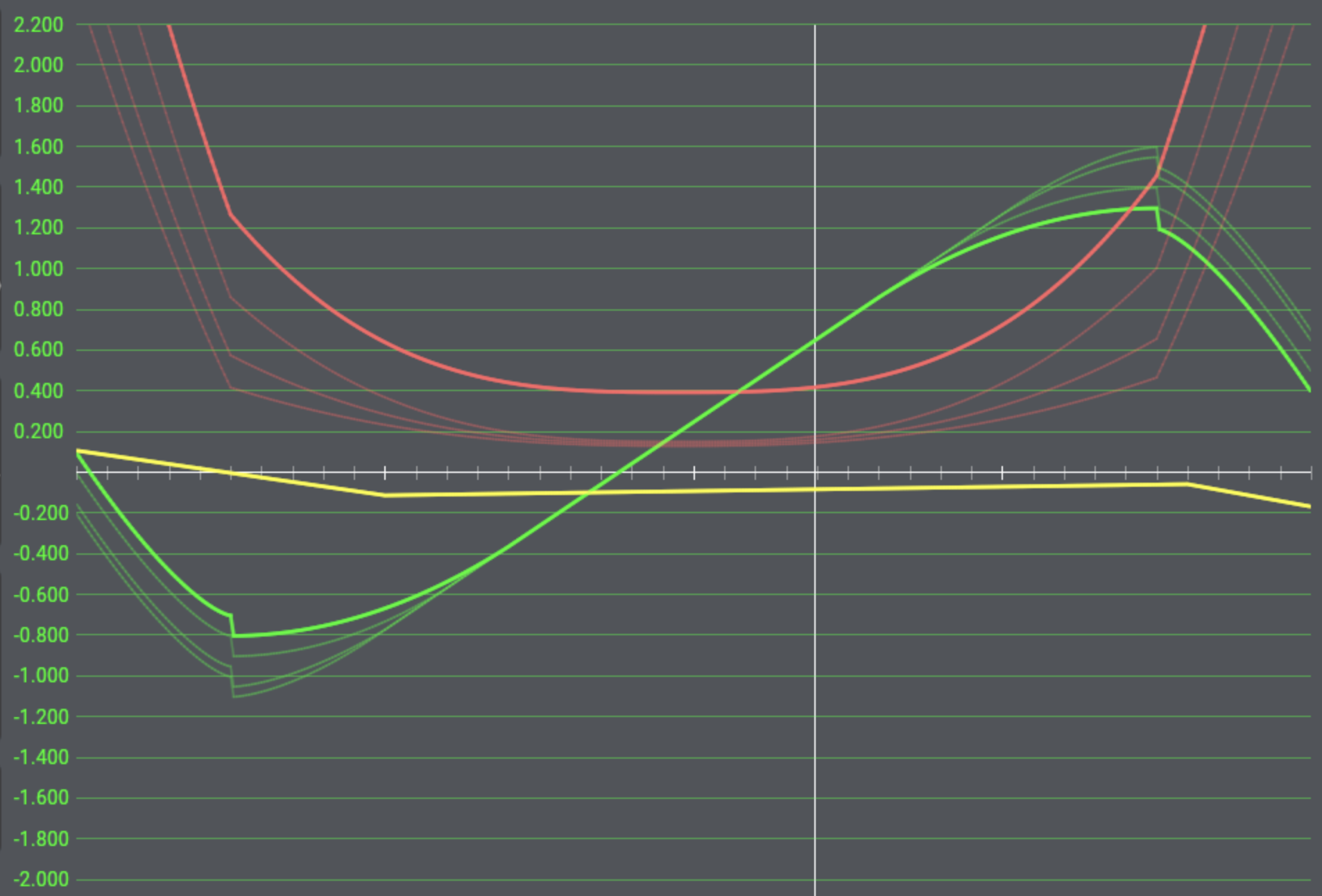
Figure 1: The graph of the airfoil’s coefficients
Moving the mouse around in the graph will cause the numbers displayed in the black box in the bottom left of the screen (seen in Figure 2) to change in real time.
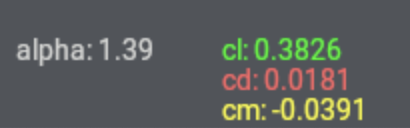
Figure 2: The coefficient display box
This is the coefficient display box which displays, for whatever spot on the graph the mouse it pointing at, the coefficients of the airfoil at that angle of attack. Just point the mouse at the part of the curve you are interested in, and look at the exact coefficients in the coefficient display box.
On the AOA-20 tab, the left edge of the graph corresponds to an angle of attack of –20°, and the right edge corresponds to an angle of attack of +20°. Therefore, moving the mouse to the left edge of the chart will cause the alpha reading in the black box to go to –20, corresponding to the –20° angle of attack. The same goes for the right edge with its +20° angle of attack. Select the AOA-180 tab to see the coefficients from -180° to +180°.
The center of the chart represents an angle of attack of zero degrees. (Remember that the angle of attack is the angle of the wing to the air. It is the angle at which the wing hits—attacks—the air).
The green line in the graph is the coefficient of lift, called cl in the coefficient display box in the bottom left. The red line is the coefficient of drag, called cd in the coefficient display box. The yellow line is the coefficient of moment, called cm in the coefficient display box. We’ll look at the behavior of each of these lines below.
Reynolds Number
In the upper left of the screen is a number labeled Re, for Reynolds number, as highlighted in Figure 3.
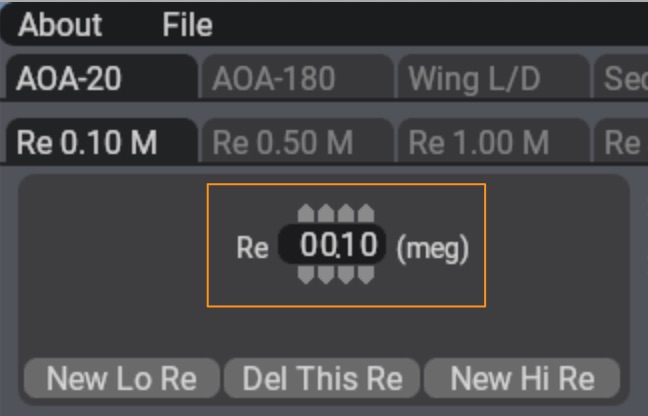
Figure 3: The Reynolds number parameter
The Reynolds number is simply the air density times the speed of the airplane times the chord of the wing divided by the viscosity of air (wow!). Experiments have shown that a wing’s coefficients of lift, drag and moment vary somewhat with Reynolds number. For recreational purposes, we can probably neglect any change in performance with Reynolds number, thus ignoring this setting altogether. The number entered in the Reynolds number box may have some impact, however, on the simulation. For highest realism, users can generate two different airfoil files for the same airfoil in Airfoil Maker, each file at a different Reynolds number, and assign them both to a wing in Plane Maker! X‑Plane will figure out the Reynolds number on each piece of the plane at least 10 times per second and interpolate between the two airfoil files to give the most realistic coefficients for that flight Reynolds number.
Pilots should realize that very good accuracy can be obtained without touching the Reynolds number at all, and without generating two airfoil files for each airfoil. Most users can ignore the above paragraph and the “Reynolds number” slot in the airfoil generation screen without sacrificing a good simulation.
In this section, we also have the thickness ratio and the drag-divergence Mach number. Thickness only affects the visual appearance of the wing when it is shown in Plane Maker and X‑Plane. The thickness ratio is an important characteristic of the airfoil so it is usually easy to find in the airfoil data or even the airfoil name. NACA 2412 has a thickness of 12% so you would enter 0.120 here.
Drag div Mach is the airspeed when drag starts to increase dramatically. The Mach number is a fraction of the speed of sound. Hence, 0.75 is 75% of the speed of sound or about 750 km/h. Most aircraft never get close to this speed so you don’t need to set this number for your airfoil. If you are designing a near-supersonic aircraft like an airliner or a supersonic aircraft then you will either need to find this number in the published specifications or adjust it until you get the resulting performance you want in X-Plane.
Coefficients

Figure 4: A graph of an airfoil’s coefficients
Coefficient of Lift
The green line in Figure 4 is the coefficient of lift.
Notice that at zero degrees angle of attack (the center of the graph) the coefficient of lift is fairly low; it is close to the thin white line that represents zero. As the angle of attack increases, the coefficient of lift increases right along with it, until it reaches around 16° angle of attack, at which point the coefficient of lift falls abruptly. That represents the stall. Looking at the negative angles of attack, one sees that the coefficient of lift actually gets negative. If you go to a large enough negative angle of attack, the airfoil stalls then, too. It is possible to stall upside down! A good wing will have a decent coefficient of lift (maybe 0.4) at angles of attack close to zero, and a nice high coefficient of lift (maybe 1.6) at the maximum angle of attack. A safe airfoil will also have a stall that is not too abrupt. In other words, the coefficient of lift will fall off gradually at the stall, rather than sharply.
Coefficient of Drag
The red line on the graph in Figure 4 is the coefficient of drag.
Notice that the coefficient of drag is lowest close to zero degrees angle of attack. The drag gets higher and higher as the wing goes to larger and larger angles of attack. That is not surprising, is it? The higher the angle the wing is offset from the airflow, the greater the drag!
It doesn’t matter much whether the wing moves to positive or negative angles of attack (that is, whether the wing is aimed up or down); moving the wing away from its most streamlined position increases its drag. A good airfoil will obviously have the lowest drag possible. (Notice that this drag coefficient does not include the drag due to the production of lift. X‑Plane will figure this drag out automatically).
Coefficient of Moment
The yellow line in the graph in Figure 4 is the coefficient of moment.
The coefficient of moment is the tendency of the wing to pitch up about its axis, or rotate upwards about the spar. Most wings actually want to pitch down, so the coefficient of moment is usually negative. The moment varies a bit with angle of attack, often in ways that are a little bit surprising. Typically the moment will be negative for all normally encountered angles of attack, decreasing (that is, becoming more negative) especially as the angle of attack is increased. This continues until the stall, at which point the moment heads back to zero. A desirable characteristic of an airfoil is usually to have a low coefficient of moment.
General Information
Finding Coefficients
Many users wonder how to find what the coefficients are for the airfoils of their own airplane. To do this, the user must first find what airfoil the aircraft uses, probably from the manufacturer. Then, check to see if that airfoil is included with X‑Plane. If a user is flying a Cessna 182, for example, that aircraft uses the NACA 2412 airfoil, which is included. Cessna 182 owners, then, do not need to generate their own airfoil for that wing. Users who do not know what airfoil to use should leave them as the defaults of Plane Maker.
Recommended Background Reading
Airfoil selection is a fun and interesting process, because one looks for the best possible combination of lift, drag, and moment characteristics for a particular airplane. For users that will be experimenting with their own airplane designs and are new to the matters discussed in this chapter, we highly recommend the following book to get started:
R/C Model Airplane Design
A.G. Lennon
Motorbooks International Publishers and Wholesalers, Inc.
The book is intended for radio control designs, but is very straightforward, easy to understand, and all of the principles apply to full-scale aircraft.
Once you understand the basics of airfoil theory and nomenclature, we recommend:
Theory of Wing Sections
Abbot and Von Doenhoff
McGraw-Hill, New York (1949)
An oldie but goodie! This book has the lift, drag, and moment plots of many airfoils in it, so the reader can choose their favorite airfoil for a design and then enter it into the computer using the technique described below.
Types of Airfoils
In the following discussion, thin and symmetrical, thick and highly cambered, and “normal general aviation” airfoils will be discussed. These types of airfoils serve as a good introduction because they are so different from one another.
Thin, symmetrical airfoils are thin and have the same shape on both the top and bottom surfaces. They do not produce very much lift or drag. They typically are used for vertical stabilizers and often horizontal stabilizers as well because they are not called upon to produce a lot of lift, and are not expected to produce much drag, either.
Use thick, high-cambered airfoils in the foreplanes of canards, or other applications where you want a large amount of lift from a small wing area. These foils are known for providing a large amount of drag as the penalty for providing a large amount of lift.
So-called “normal general aviation airfoils,” like the NACA 2412 (seen in Figure 5), are compromises between the two, and are good candidates for the wing of a general aviation aircraft.

Figure 5: A NACA 2412 airfoil
Supercritical, laminar-flow, and other possible groupings of airfoils exist, but for the purposes of our discussion we will concentrate on the thin and symmetrical, thick and highly cambered, and “normal general aviation” airfoils just outlined.
Generating Airfoils
Coefficient of Lift Intercept
Now let’s actually generate an airfoil. The control to modify first is the coefficient of lift intercept control, found in the upper left, as highlighted in Figure 6.
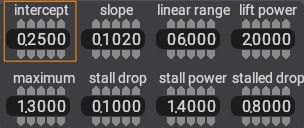
Figure 6: The parameters used in generating an airfoil
To increase this number, you can click right above the digits that you want to increase, and below the ones that you want to decrease. For example, if the lift intercept on the screen is 0.25 (as in Figure 6), and you want to change it to 0.33 to model your airfoil, just click above the “2” in “0.2500” and twice below the “5” in “0.2500.” Alternatively, you can click in the box and type the number you’d like to have. Use either of these two ways to change all of the data for the entire design and simulation system.
The coefficient of lift intercept is the coefficient of lift at an angle of attack of 0 degrees. For a symmetrical airfoil, this will always be zero, since, in such an airfoil, the air is doing exactly the same thing on the top and bottom of the wing at zero degrees angle of attack. Symmetrical airfoils are sometimes used for horizontal stabilizers, and are almost always used for vertical stabilizers. Sleek, skinny wings with low camber might have a lift intercept of 0.1. Fat, highly cambered foils have a value around 0.6. A typical airfoil like the NACA 2412 (commonly used in general aviation) has a value of about 0.2.
Coefficient of Lift Slope
This is the increase in coefficient of lift per degree increase in angle of attack. A thin airfoil has a value of about 0.1. A really fat airfoil has a value of about 0.08. Fatter airfoils have slightly lower lift slopes. (You will find, however, that lift slopes are almost always very close to 0.1.)
The coefficient of lift slope is modified using the slope control, seen in Figure 6.
Coefficient of Lift Curvature Near the Stall
As the angle of attack gets close to stall, the lift slope is no longer linear. Instead, it gradually levels off as it approaches the maximum, or stalling, coefficient of lift.
This value is modified by the first power control, seen in Figure 6.
Just play with this control until you find a power curve that connects the linear and stalling regions smoothly. Chances are a power of around 1.5 will work pretty well. Just play with it until the lift comes up smoothly, then gradually levels off to the stall, since that is what happens with a real airfoil.
Coefficient of Lift Maximum
This is the maximum coefficient of lift, or the coefficient of lift right before the stall. A very thin, symmetrical airfoil has a value of around 1.0. A thick, highly cambered airfoil has a value of around 1.8. A typical general aviation foil might have a value of around 1.6.
This value is modified using the maximum control, seen in Figure 6.
Coefficient of Lift Immediate Drop at Stall
This is the drop in lift that immediately follows the stall. For thin airfoils, which tend to stall sharply, this value might be 0.2. For many airfoils, however, there is no immediate drop, but instead a more gradual one as the angle of attack is further increased. In most cases, this number will be zero or very close to zero.
This is modified using the drop control, seen in Figure 6.
Coefficient of Lift Curvature After the Stall
Different airfoils have different lift slopes after the stall. For skinny airfoils that stall sharply, the power should be fairly low, perhaps around 1.4. For fat airfoils (which usually have more gentle stalling characteristics) this number may be closer to 2.0.
This setting is controlled via the box, seen in Figure 6.
Just play with the second power control until the graph looks like the data you are trying to model from the airfoil chart in whatever book you are getting your airfoil data from.
Coefficient of Lift Drop from Stall to 20 Degrees
This is the decrease in coefficient of lift from the stall to an angle of 20°. This number, modified using the second drop control seen in Figure 6, might be in the 0.4 range for a thicker airfoil, 0.6 for a thinner one. The NACA 2412 has a value of about 0.4. (The coefficient of lift goes from around 1.6 to 1.2 as the angle of attack goes from around 16° to 20°.)
Coefficient of Drag Minimum
The coefficient of drag minimum, labeled cd-min in Figure 7, is the minimum coefficient of drag of the airfoil. Once again, this does not include induced drag, which is determined automatically by the X‑Plane simulator.
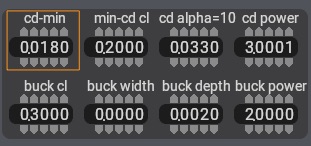
Figure 7: Further specifications for an airfoil’s constants
This minimum coefficient of drag also should not include the “low-drag bucket” of a laminar flow wing. A thick or highly cambered airfoil has a value of about 0.01. A typical older general-aviation airfoil such as the NACA 2412 has a value of about 0.006, and a really thin, symmetrical airfoil has about a 0.005 value. Laminar flow airfoils can approach values of 0.004, but that number should not be entered here, because it will be addressed in the laminar drag bucket controls discussed below.
Coefficient of Lift at Which Minimum Drag Occurs
Enter the coefficient of lift at which the minimum drag occurs in the min-d cl control, seen in Figure 7. This value is probably very close to the coefficient of lift at zero degrees angle of attack, called the lift intercept—the very first number we entered. If anything, the minimum coefficient of drag occurs at a coefficient of lift a little lower than the lift intercept coefficient of lift. This is because an airfoil usually has the least drag at an angle of attack of about zero degrees or just a hair lower.
Coefficient of Drag at Angle of Attack of 10 Degrees
This value is modified using the d alpha=10 control seen in Figure 7. For a thin, symmetrical airfoil, this value might be around 0.015. The NACA 2412 comes in with a surprisingly good 0.012. A really highly cambered airfoil might be around 0.025, though.
Coefficient of Drag Curvature
This value is set by the first power control in the drag section, seen in Figure 7. The power curve is simply the curvature of the drag curve as it changes with angle of attack. You will have to fiddle with the curvature until the curve looks like the experimental data, but theoretically this number will be around 2.
Laminar Drag Bucket Location
Some airfoils, called “natural laminar flow” or “NLF” airfoils, have perfectly smooth airflow across a large part of the wing. This flow pattern is called “laminar flow” (hence the company name “Laminar Research”). This super smooth, low-drag flow can only happen at fairly small angles of attack, though, so there is a “low-drag bucket,” or area in a small angle of attack range, that has lower-than-normal drag. The drag bucket location is usually thought of in terms of the coefficient of lift. In other words, the center of the drag bucket occurs at some coefficient of lift of the airfoil. This might happen at a coefficient of lift of around 0.6.
The laminar drag bucket location is set using the cl location control, seen in Figure 7.
Laminar Drag Bucket Width
The laminar drag bucket width, set using the width control (shown in in Figure 7), refers to how “wide” the bucket is, or what range of coefficient of lift the drag bucket covers. A decent guess would be 0.4.
Laminar Drag Bucket Depth
This is the all-important variable. The depth control, seen in Figure 7, determines how much the airfoils drag is reduced by going to laminar flow. Ideally, this will be around 0.002. That is actually quite a bit, though; it might turn a coefficient of drag of 0.006 to 0.004—quite a large percentage difference.
Laminar Drag Bucket Curvature
This is set using the second power control in the drag section of the window, seen in Figure 7. The power curve is simply the curvature of the low drag bucket. You will have to fiddle with the curvature until the curve looks like the experimental data, but chances are this number will be around 3 to 5.
Coefficient of Moment Low-Alpha Change Point
The coefficient of moment is usually linear across the non-stalled angle of attack range. In other words, if the airfoil is not stalled, the moment curve is usually a straight line. After the stall, however, the moment coefficient tends to change direction. For the NACA 2412, the moment coefficient has its low angle of attack moment change at 10°, a point corresponding to roughly +4° before the stall.
This point of change is set using the alpha 1 control highlighted in Figure 8.

Figure 8: Further specifications for an airfoil’s constants
Coefficient of Moment High-Alpha Change Point
This characteristic, set using the alpha 2 control (seen in Figure 8), determines where the moment coefficient changes direction with a positive angle of attack. The NACA 2412 airfoil has its high angle of attack moment-change right at the positive stalling angle of 16°.
Coefficient of Moment at 20 Degrees
This is set using the cm 1 control, seen in Figure 8.
For the NACA 2412, this number is about 0.075. Notice that this is a positive number. This means that if the airfoil is at a clear negative angle of attack, it will stall and try to pitch back up to an angle of attack closer to zero. This is a nice effect, because the airfoil tends to try and recover from the stall automatically.
Coefficient of Moment at Low-Alpha Change Point
This is set using the cm 2 control, seen in Figure 8. For the NACA 2412, this number is about –0.05, which is a light pitch-down. A wing with a higher camber will have a value of around –0.10, perhaps even –0.13. A symmetrical airfoil will have no pitch tendency at all here, so 0.0 should be entered for that type of airfoil.
Coefficient of Moment at High-Alpha Change Point
This is set using the cm 3 control, seen in Figure 8. For the NACA 2412, this number is about 0.025, which is a very light pitch-down. A wing with a higher camber will have a value of around 0.10, perhaps even 0.13. A symmetrical airfoil will have no pitch tendency at all here, so 0.0 should be entered for that type of airfoil.
Coefficient of Moment at 20 Degrees
This is the coefficient of moment well into the stall, set using the cm 4 control seen in Figure 8. For the NACA 2412, it is about –0.10. This is a moderate pitch-down, which is desirable because this pitch-down will help recover from the stall.
Stall Minimum and Maximum Angle of Attack

Figure 9: Specifications for an airfoil’s AoA at stall
The final two fields seen in Figure 9 specify the minimum and maximum angles of attack at which the airfoil stalls and loses lift, respectively.
Finishing Up
Change all of the parameters around a bit as discussed above, then select Save As from the File menu. Type in an airfoil name and hit Enter. Congratulations! You have just generated your own airfoil! Drop it in the Airfoils folder in your X‑Plane folder (so that it will be usable by all planes), or in a folder that you make called “Airfoils” in the same folder as your airplane designs (to be used only by that airplane).
Other Airfoil Maker Screens
There are three other pages of information in Airfoil Maker. These are not required to make a successful airfoil, but you would probably look at them at least once during the development of an airfoil.
–180 to +180° Coefficients
Figure 10: A graph of the -180 to 180 degree coefficients
This window of the AOA-180 tab is just an information display. This shows the complete airfoil coefficients from –180° to +180°. These coefficients would only be used if you were flying backwards or some other unusual attitude.
If you change any of the parameters on the left, you will see that all of the editing you did above was only working on the small section from –20 to +20°. There is normally no need to change the coefficients outside this range because it doesn’t matter if your airfoil was designed by Boeing or by Airbus; the performance of any airfoil is about the same when your plane is fluttering through the air like a falling leaf.
It is possible to change these values by editing the .afl text file directly but that is only useful if you have a gigantic amount of data on your airfoil. If you do do that, then never open the .afl file in Airfoil Maker as it will overwrite your coefficients with its own in the +/–20° region. The intercept/slope/power numbers are not used by the simulator, only the tabulated coefficients.
Wing L/D
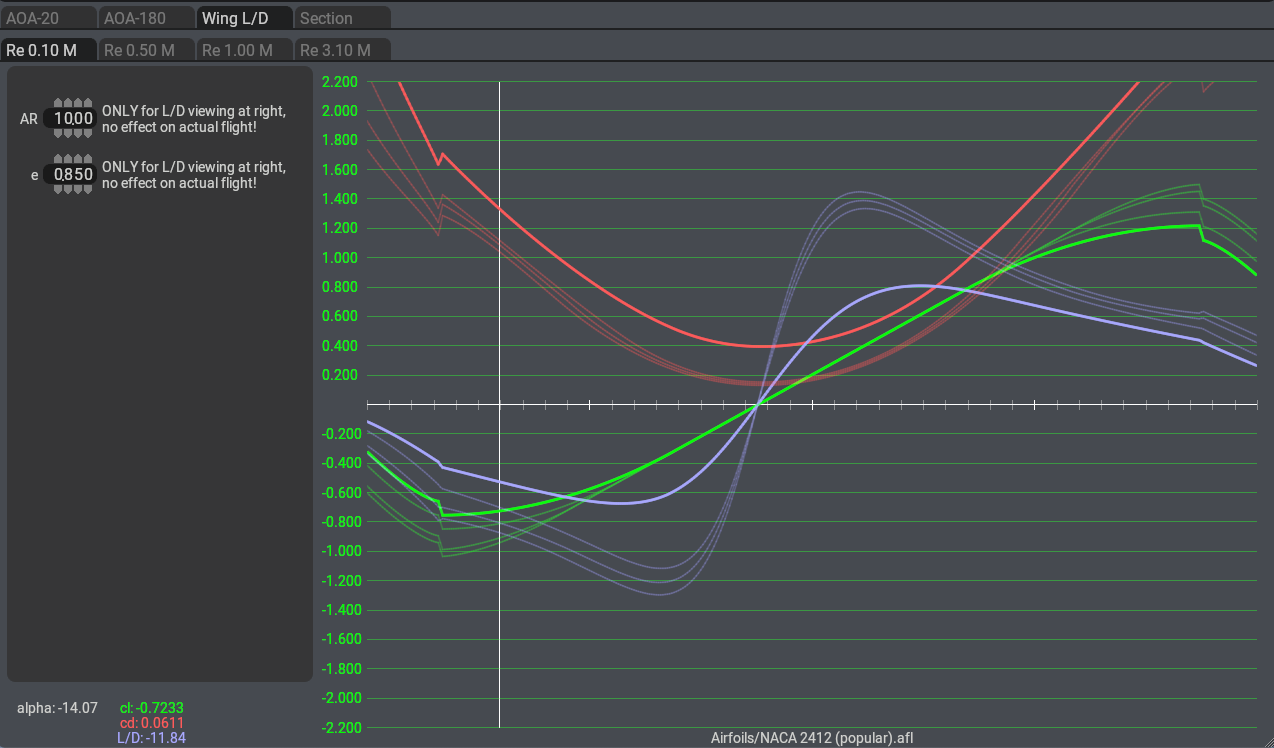
Figure 11: The Wing L/D tab
This is another information page. It is useful to check the results of your entries by calculating the L/D (lift over drag ratio) for a hypothetical wing. Remember the coefficients on the previous pages are never found in real life because they refer to an imaginary wing of infinite length. Even wind tunnel data must be corrected for the effect of only having a specific length of the theoretical infinite wing.
Enter the aspect ratio (AR) for your plane and the efficiency factor e. A glider or U–2 Dragon Lady with extremely long wings might have an aspect ratio of 30. A light aircraft such as a Cessna 180 has an aspect ratio of 7.3. The aspect ratio of a straight wing is the wingspan divided by the chord. For any other shape of wing, the easiest way to calculate AR is to square the wing span and divide by the wing area: AR = s2/A.
Section
The section page is used to influence the visual representation of the wing profile in X‑Plane. Many real wings are almost flat on the bottom or have different bulges to the typical airfoil.
Figure 12: A view of the wingfoil’s camber
This has no effect on the way the plane flies in X-Plane—it is only for the visual model. There are only a couple of points here, so you can’t make a detailed 3-D model of your wing. There should be enough adjustment here so that a model of a Concorde wouldn’t look completely silly with fat wings.
The yellow lines visually indicate the thickness ratio which you set on the first page.
If you are modeling an aircraft that has different airfoils at different positions along the wing span you need to pay attention to this camber page. Each wing can have a different airfoil at the root and the tip and X‑Plane smoothly interpolates between them. If two X‑Plane wing segments are attached together root-to-tip then there will be an obvious step if the two cambers don’t match. Either use the same camber in both airfoil files (difficult) or always make sure the tip airfoil of the inner wing uses exactly the same airfoil file as the root airfoil of the outer wing section.
This feature can also be useful when you need to make small fairings or fittings out of dummy wings. Engine Pylons, Misc Bodies or Misc Objects should be considered first but sometimes a small stub wing is required. Remember a pylon or a misc body is a Plane Maker body like a fuselage which contributes to the simulated drag on the aircraft. An object is a 3-D model produced in an external modeling program which is just a visual effect with no aerodynamics. But a wing can also produce lift, roll or yaw, affecting the plane’s flight path.